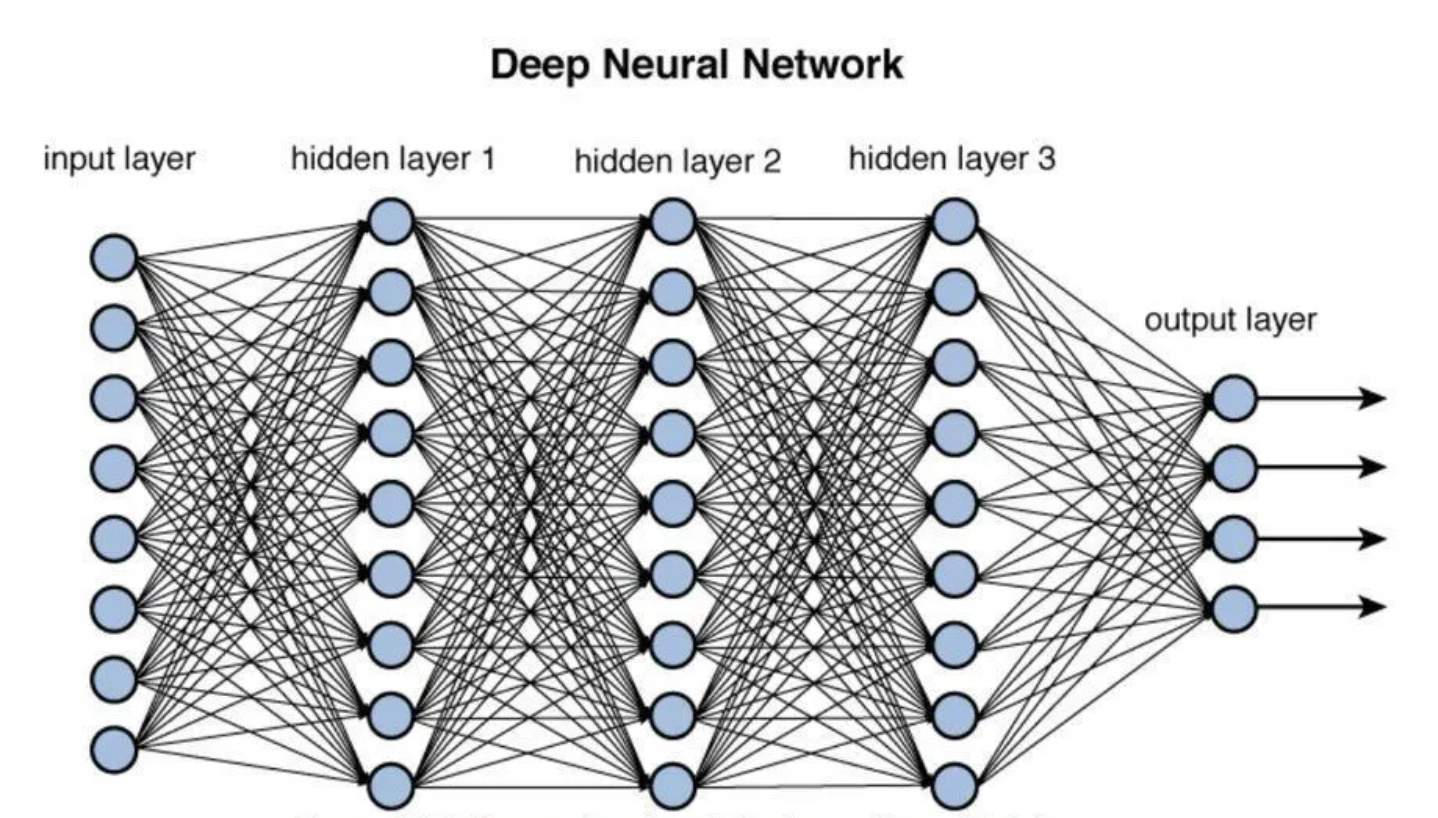
심층 신경망(Deep Neural Network)

심층 신경망(Deep Neural Network, DNN)은 여러 개의 은닉층을 포함하는 인공 신경망의 한 종류이다. 인공 신경망은 입력층(input layer), 하나 이상의 은닉층(hidden layers), 그리고 출력층(output layer)으로 구성되며, 이 중에서 은닉층이 여러 개인 경우를 심층 신경망이라고 한다. 심층 신경망은 복잡한 데이터에서 높은 수준의 추상화와 패턴 인식을 수행할 수 있으며, 이미지 인식, 자연어 처리, 음성 인식 등 다양한 분야에서 광범위하게 활용된다.

[출처 : 혼자 공부하는 머신러닝+딥러닝 7장. 인공 신경망]

심층 신경망의 특징:

• 다층 구조: 심층 신경망은 두 개 이상의 은닉층을 가진다. 은닉층의 수가 많을수록 네트워크는 더 복잡한 패턴과 관계를 학습할 수 있다.
• 비선형성: 심층 신경망은 비선형 활성화 함수를 사용하여 입력 데이터의 비선형 특성을 모델링한다. 이를 통해 선형 모델로는 표현할 수 없는 복잡한 패턴을 학습할 수 있다.
• 자동 특성 추출: 심층 신경망은 데이터로부터 중요한 특성을 자동으로 학습하고 추출할 수 있다. 이는 수동으로 특성을 설계하는 작업을 줄여준다.
• 범용 근사자: 이론적으로 심층 신경망은 어떤 함수도 근사할 수 있는 범용 함수 근사자(universal function approximator)로 간주된다.

활용 분야:

• 컴퓨터 비전: 이미지 분류, 객체 탐지, 이미지 생성 등에 활용된다.
• 자연어 처리: 기계 번역, 감성 분석, 텍스트 요약 등의 작업에 사용된다.
• 음성 인식: 음성을 텍스트로 변환하거나, 음성 명령을 인식하는 데 사용된다.
• 게임 및 로봇 공학: 자율 주행, 게임 AI, 로봇의 의사 결정 등에 활용된다.

도전 과제:

• 과적합(Overfitting): 모델이 훈련 데이터에 지나치게 최적화되어 새로운 데이터에 대한 일반화 능력이 떨어질 수 있다.
• 해석성(Interpretability): 심층 신경망의 결정 과정이 “블랙 박스”처럼 보일 수 있어, 모델의 예측을 해석하기 어려울 수 있다.
• 계산 비용: 심층 신경망의 학습은 대량의 데이터와 고성능의 컴퓨팅 자원을 요구한다.

이제 여러 개의 층을 추가하여 다층 인공 신경망, 즉 심층 신경망을 만들고, 은닉층에 사용하는 활성화 함수인 렐루 함수, 가중치와 절편을 학습하기 위한 옵티마이저를 알아본다.

1. 데이터 준비

데이터를 표준화 전처리하고 훈련세트와 검증세트로 나눈다.

from tensorflow import keras
from tensorflow import keras
from sklearn.model_selection import train_test_split

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()

train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28)
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)

2. 시그모이드 함수로 밀집층 추가하기

인공 신경망과 달리, 입력층과 출력층 사이에 밀집층을 추가한다. 이를 은닉층이라고 한다.

2-1. 은닉층의 활성화 함수 : 시그모이드

인공 신경망에서 출력층에 적용했던 소프트맥스 함수도 활성화 함수이다.
단 출력층에서는 보통 이진 분류에서는 시그모이드 함수, 다중 분류에서는 소프트맥스를 사용한다.
은닉층에도 활성화 함수가 적용되는데, 대표적으로 시그모이드 함수와 볼 렐루 함수가 있다.

은닉층 활성화 함수를 적용하는 이유는 선형 계산을 비선형으로 비틀어 주어 다음 층의 계산과 합쳐지지 않고 역할을 수행할 수 있기 때문이다.

아래 그림은 시그모이드 그래프이다.

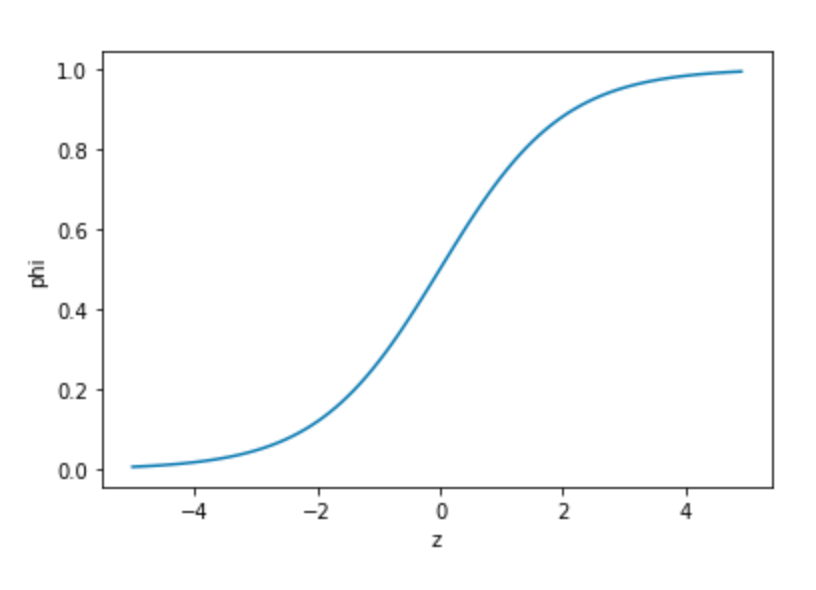
이 함수는 뉴런의 출력 z값을 0과 1사이로 압축한다. 이를 사용해 은닉층을 만든다.

2-2. 시그모이드 활성화 함수로 심층 신경망 생성하기

dense1 = keras.layers.Dense(100, activation='sigmoid', input_shape=(784,))

#출력층에서 10개의 클래스를 분류하므로 10개의 뉴런, 소프트맥스 활성화함수
dense2 = keras.layers.Dense(10, activation='softmax')

activation='sigmoid'로 활성화 함수를 시그모이드로 지정할 수 있다.
은닉층에서 100개의 뉴런을 지정했는데, 이는 특별한 기준이 없지만, 출력층의 뉴런보다는 많이 만들어야한다.

이제 위의 두 개층을 Sequential 클래스에 추가하여 심층 신경망을 만든다.
두 개의 층을 리스트로 Sequential 클래스에 전달한다.

model = keras.Sequential([dense1, dense2])
model.summary()

Model: "sequential_2"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 100)               78500     
 dense_1 (Dense)             (None, 10)                1010      
=================================================================
Total params: 79,510
Trainable params: 79,510
Non-trainable params: 0
_________________________________________________________________

summary() 메서드로 층에 대한 정보를 얻는다.

dense의 출력 크기를 보면 (None, 100)으로, 첫번째 차원은 샘플 크기를 나타낸다. 샘플 갯수가 아직 정의되지 않아 None 이며, 후에 fit() 매서드에 훈련 데이터를 주입하면 미니배치 경사 하강법을 사용한다.
케라스의 기본 미니베치 크기는 32개이며, fit() 메서드에서 batch_size 매개변수로 바꿀 수 있다.

두번째 100개 출력은, 784개의 특성이 은닉층을 통과하며 100개의 특성으로 압축됨을 뜻한다.

모델 파라미터 갯수는 입력픽셀 784개와 100개의 모든 조합에 대한 가중치, 100개의 절편이 있어 784*100 + 199 = 78500개 이다.

두번째 층의 파라미터 또한 100*10 + 10 = 1010개 이다.

2-3. 층을 추가하는 다른 방법

Sequential 클래스의 생성자 안에서 바로 Dense 클래스의 객체를 만드는 방법이 있다.

model = keras.Sequential([
                          keras.layers.Dense(100, activation='sigmoid', input_shape=(784,), name='hidden'),
                          keras.layers.Dense(10, activation='softmax', name="output")
], name='패션 MNIST모델')

너무 많은 층을 추가하려면 생성자가 매우 길어지기 때문에, add() 메서드도 사용한다.

model = keras.Sequential()
model.add(keras.layers.Dense(100, activation='sigmoid', input_shape=(784,)))
model.add(keras.layers.Dense(10, activation='softmax'))

2-4. 심층 신경망 모델 훈련

model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)

Epoch 1/5
1500/1500 [==============================] - 5s 3ms/step - loss: 0.5596 - accuracy: 0.8103
Epoch 2/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.4054 - accuracy: 0.8556
Epoch 3/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.3716 - accuracy: 0.8658
Epoch 4/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.3489 - accuracy: 0.8735
Epoch 5/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.3320 - accuracy: 0.8801

추가된 층이 성능을 항상시켰다는 것을 알 수 있다.

3. 렐루 활성화 함수

초창기 인공 신경망의 은닉층에 많이 사용된 활성화 함수는 시그모이드 함수였다.
다만 이 함수는 오른쪽과 왼쪽 끝으로 갈수록 그래프가 누워있기 때문에 올바른 출력을 만드는데 신속하게 대응하지 못한다는 단점이 있다. 이는 층이 많은 신경망일수록 효과가 누적되어 학습을 어렵게 한다.

이를 개선하기 위해 렐루함수가 사용된다.

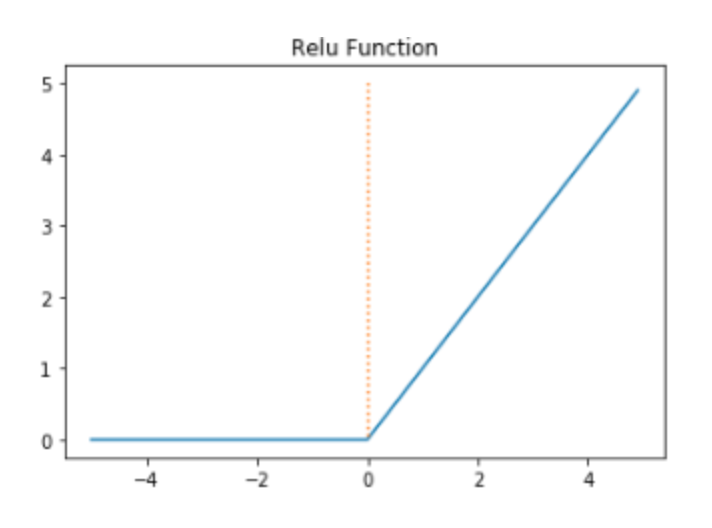
렐루 함수는 max(0,z)로 쓸 수 있다. 이는 특히 이미지 처리에 좋은 성능을 낸다.

3-1. 입력 차원을 일렬로 펼치는 Flatten 층

렐루 함수를 적용하기 전, 입력차원을 일렬로 펼치는 Flatten 층을 알아본다.
앞에서 reshape() 메서드를 사용하여 사진 데이터를 일렬로 펼쳤지만, 이를 입력층과 은닉층 사이에 추가할 수 있다.

model.add(keras.layers.Flatten(input_shape=(28, 28)))

3-2. 렐루 함수를 이용한 밀집층 추가

model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))

model.summary()

Model: "sequential_4"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 flatten (Flatten)           (None, 784)               0         
 dense_4 (Dense)             (None, 100)               78500     
 dense_5 (Dense)             (None, 10)                1010      
=================================================================
Total params: 79,510
Trainable params: 79,510
Non-trainable params: 0
_________________________________________________________________

Flatten 층을 신경망 모델에 추가하면 입력값의 차원을 짐작할 수 있다.

3-3. 훈련 데이터로 모델 훈련

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
train_scaled = train_input / 255.0
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)

model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)

Epoch 1/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.5249 - accuracy: 0.8142
Epoch 2/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.3924 - accuracy: 0.8590
Epoch 3/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.3553 - accuracy: 0.8712
Epoch 4/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.3310 - accuracy: 0.8810
Epoch 5/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.3179 - accuracy: 0.8868

검증 세트로 모델을 평가해본다.

model.evaluate(val_scaled, val_target)

375/375 [==============================] - 1s 2ms/step - loss: 0.3948 - accuracy: 0.8674
[0.39478805661201477, 0.8674166798591614]

은닉층을 추가하지 않은 모델보다 성능이 몇 퍼센트 더 상승했다.

4. 옵티마이저 : 다양한 경사 하강 알고리즘

신경망에는 모델이 학습되지 않아 사람이 지정해주어야 하는 하이퍼파라미터가 많다. 다양한 종류의 경사 하강법 알고리즘도 지정할 수 있는데, 이를 옵티마저라고 한다.

4-1. SGD : 확률적 경사 하강법

compile() 메서드에서 케라스의 기본 경사 하강법 알고리즘은 RMSprop을 사용했다.
확률적 경사 하강법인 SGD를 사용할 수 있는데, 이 역시 미니배치를 사용한다.

model.compile(optimizer='sgd', loss='sparse_categorical_crossentropy', metrics='accuracy')

SGD 객체를 생성하여 옵티마저로 적용할 수 있다.

sgd = keras.optimizers.SGD()
model.compile(optimizer=sgd, loss='sparse_categorical_crossentropy', metrics='accuracy')

SGD 클래스의 학습률 기본값은 0.01이며, learning_rate 매개변수에 학습률을 지정할 수 있다.

sgd = keras.optimizers.SGD(learning_rate=0.1)

momentum 매개변수의 기본값은 0이고 0보다 큰 값으로 지정하면 그레디언트를 가속도처럼 사용하는 모멘텀 최적화를 사용할 수 있다. 보통 0.9 이상을 지정한다.
nesterov 매개변수를 True로 바꾸면 네스테로프 모멘텀 최적화를 사용한다.

sgd = keras.optimizers(momentum=0.9, nesterov=True)

네스테로프 모멘텀은 모멘텀 최적화를 두번 반복하여 구현한다. 대부분 기본 확률적 경사 하강법보다 나은 성능을 제공한다.

4-2. Adagrad, RMSprop : 적응적 학습률 사용

모델이 최적점에 가까이 갈수록 학습률을 낮출 수 있으며, 이를 통해 안정적으로 최적점에 수렴할 가능성이 높다.

adagrad = keras.optimizers.Adagrad()
model.compile(optimizer=adagrad, loss='sparse_categorical_crossentropy', metrics='accuracy')

rmsprop = keras.optimizers.RMSprop()
model.compile(optimizer=rmsprop, loss='sparse_categorical_crossentropy', metrics='accurac')

모멘텀 최적화와 RMSprop 장점을 접목한 것이 Adam이다.

4-3. Adam : 모멘텀 최적화와 RMSprop의 장점 접목

Adam 클래스의 매개변수 기본값을 사용해 모델을 훈련한다.

model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28,28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))

# 옵티마이저를 Adam으로 훈련
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)

Epoch 1/5
1500/1500 [==============================] - 4s 2ms/step - loss: 0.5218 - accuracy: 0.8183
Epoch 2/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.3916 - accuracy: 0.8586
Epoch 3/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.3544 - accuracy: 0.8711
Epoch 4/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.3248 - accuracy: 0.8809
Epoch 5/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.3058 - accuracy: 0.8880

검증 세트에서의 성능도 확인해본다.

model.evaluate(val_scaled, val_target)

375/375 [==============================] - 1s 2ms/step - loss: 0.3426 - accuracy: 0.8767
[0.3426271080970764, 0.8767499923706055]