지도 학습과는 달리 정답 라벨이 없는 데이터를 비슷한 특징끼리 군집화하여 새로운 데이터에 대한 결과를 예측하는 방법을 비지도학습이라고 한다.
라벨링 되어있지 않은 데이터로부터 패턴이나 형태를 찾아야 하기 때문에 지도학습보다는 조금 더 난이도가 있다고 할 수 있다.
실제로 지도 학습에서 적절한 피처를 찾아내기 위한 전처리 방법으로 비지도 학습을 이용하기도 한다.

[출처 : 혼자 공부하는 머신러닝+딥러닝 6장. 비지도 학습]

비지도학습

비지도학습의 대표적인 종류는 클러스터링(Clustering)이 있다. 이 외에도 Dimentionality Reduction, Hidden Markov Model이 있다.
예를 들어 여러 과일의 사진이 있고 이 사진이 어떤 과일의 사진인지 정답이 없는 데이터에 대해 색깔이 무엇인지, 모양이 어떠한지 등에 대한 피러르 토대로 바나나다, 사과다 등으로 군집화 하는 것이다.

지도/비지도 학습 모델(Semi-Supervised Learning)을 섞어서 사용할 수도 있다. 소량의 분류된 데이터를 사용해 분류되지 않은 더 큰 데이터 세트를 보강하는 방법으로 활용할 수도 있다.

최근 각광받고 있는 GAN(generative Adversarial Network) 모델도 비지도 학습에 해당한다.

과일 분류하기 예시

!wget https://bit.ly/fruits_300_data -O fruits_300.npy

• 코랩의 코드 셀에서 ‘!’ 문자로 시작하면 코랩은 이후 명령을 파이썬 코드가 아니라 리눅스 쉘 명령으로 이해한다.
• wget 명령은 원격 주소에서 데이터를 다운로드하여 저장한다.

import numpy as np
import matplotlib.pyplot as plt

fruits = np.load('fruits_300.npy')

• npy 파일을 load() 메서드를 이용하여 로드한다.

>>> print(fruits.shape)
(300, 100, 100)

• 첫 번째 차원(300)은 샘플의 개수
• 두 번째 차원(100)은 이미지 높이, 세 번째 차원(100)은 이미지 너비

>>> print(fruits[0, 0, :])
[  1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   2   1
   2   2   2   2   2   2   1   1   1   1   1   1   1   1   2   3   2   1
   2   1   1   1   1   2   1   3   2   1   3   1   4   1   2   5   5   5
  19 148 192 117  28   1   1   2   1   4   1   1   3   1   1   1   1   1
   2   2   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1]

첫 번째 해에 있는 픽셀 100개에 들어 있는 값을 출력하면 위와 같다.
이 넘파이 배열은 흑백 사진을 담고 있으므로 0~255까지의 정숫값을 가진다.

이 첫 번째 이미지를 배열과 비교하기 위해 그림으로 그리면 아래와 같다.

plt.imshow(fruits[0], cmap='gray')
plt.show()

• cmap : 사용할 컬러의 스케일을 지정해줄 수 있음

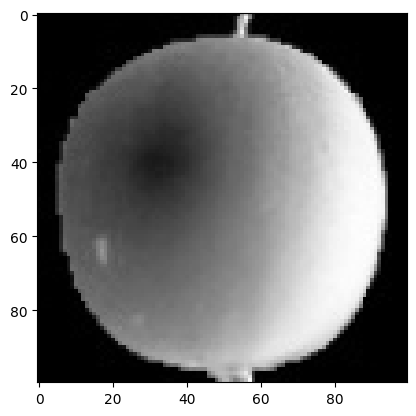
우리가 보는 것과 컴퓨터가 처리하는 방식이 다르기 때문에 위와 같이 흑백 이미지를 반전하여 사용한다.
cmap 매개변수를 ‘gray_r’로 지정하면 다시 반전하여 우리 눈에 보기 좋게 출력 가능하다.

plt.imshow(fruits[0], cmap='gray_r')
plt.show()

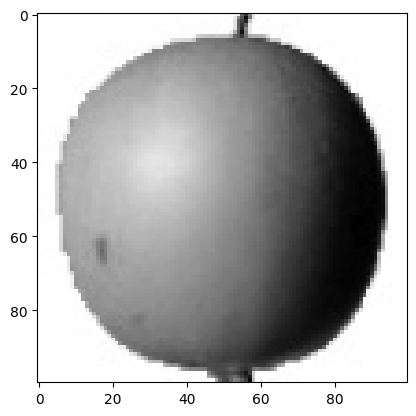
이 그림에서 밝은 부분은 0에 가깝고 짙은부분은 255에 가깝다.

픽셀값 분석하기

로드 한 데이터의 처음 100개는 사과, 그다음 100개는 파인애플, 마지막 100개는 바나나이다.
각 과일 사진의 평균을 내서 차이를 확인해보겠다.
사용하기 쉽게 fruits 데이터를 사과, 파인애플, 바나나로 각각 나눠 보겠다.

apple = fruits[0:100].reshape(-1, 100*100)
pineapple = fruits[100:200].reshape(-1, 100*100)
banana = fruits[200:300].reshape(-1, 100*100)

• reshape() 메서드를 사용해 두 번째 차원(100)과 세 번째 차원(100)을 10,000으로 합친다.
• 첫 번째 차원을 -1로 지정하면 자동으로 남은 차원을 할당한다.
• 이제 apple, pineapple, banana 배열의 크기는 100, 10000)이다.

각 배열에 들어 있는 샘플의 픽셀 평균값을 계산하기 위해 mean() 메서드를 사용하겠다.
샘플마다 픽셀의 평균값을 계산해야 하므로 mean() 메서드가 평균을 계산할 축을 지정해야 한다.
axis=0으로 하면 첫 번째 축인 행을 따라 계산한다.
axis=1로 지정하면 두 번째 축인 열을 따라 계산한다.

>>> print(apple.mean(axis=1))
[ 88.3346  97.9249  87.3709  98.3703  92.8705  82.6439  94.4244  95.5999
  90.681   81.6226  87.0578  95.0745  93.8416  87.017   97.5078  87.2019
  88.9827 100.9158  92.7823 100.9184 104.9854  88.674   99.5643  97.2495
  94.1179  92.1935  95.1671  93.3322 102.8967  94.6695  90.5285  89.0744
  97.7641  97.2938 100.7564  90.5236 100.2542  85.8452  96.4615  97.1492
  90.711  102.3193  87.1629  89.8751  86.7327  86.3991  95.2865  89.1709
  96.8163  91.6604  96.1065  99.6829  94.9718  87.4812  89.2596  89.5268
  93.799   97.3983  87.151   97.825  103.22    94.4239  83.6657  83.5159
 102.8453  87.0379  91.2742 100.4848  93.8388  90.8568  97.4616  97.5022
  82.446   87.1789  96.9206  90.3135  90.565   97.6538  98.0919  93.6252
  87.3867  84.7073  89.1135  86.7646  88.7301  86.643   96.7323  97.2604
  81.9424  87.1687  97.2066  83.4712  95.9781  91.8096  98.4086 100.7823
 101.556  100.7027  91.6098  88.8976]

• 사과 샘플 100개에 대한 픽셀 평균값을 계산한 것이다.
• 히스토그램을 그려보면 평균값이 어떻게 분포되어 있는지 한눈에 볼 수 있다.

히스토그램이란

히스토그램은 값이 발생한 빈도를 그래프로 표시한 것이다. 보통 x축이 값의 구간(계급)이고, y축은 발생 빈도(도수)이다.

plt.hist(np.mean(apple, axis=1), alpha=0.8)
plt.hist(np.mean(pineapple, axis=1), alpha=0.8)
plt.hist(np.mean(banana, axis=1), alpha=0.8)
plt.legend(['apple', 'pineapple', 'banana'])
plt.show()

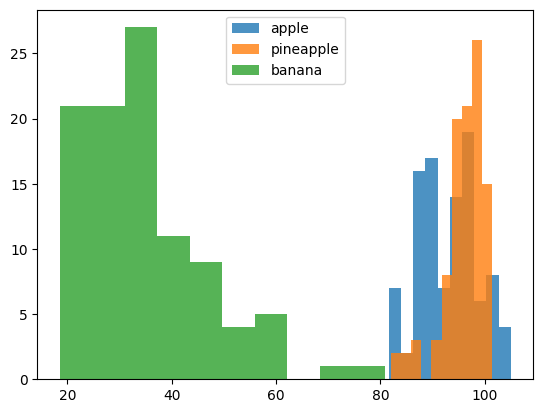
• 사과와 파인애플은 90~100 사이에 많이 모여있다.
• 바나나는 픽셀 평균값만으로 사과나 파인애플과 확실히 구분된다.
• 사과와 파인애플은 많이 겹쳐져있어서 픽셀값만으로는 구분하기 쉽지 않다.

해결책으로 샘플의 평균값이 아니라 픽셀별 평균값을 비교하는 방법이 있다.
전체 샘플에 대해 각 픽셀의 평균을 계산하는 것이다.
픽셀의 평균을 계산하는 것은 axis=0으로 지정하면 된다.

fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].bar(range(10000), np.mean(apple, axis=0))
axs[1].bar(range(10000), np.mean(pineapple, axis=0))
axs[2].bar(range(10000), np.mean(banana, axis=0))
plt.show()

• 순서대로 사과, 파인애플, 바나나 그래프이다.
• 각 과일마다 값이 높은 구간이 다르다.

픽셀 평균값을 100*100 크기로 바꿔서 이미지처럼 출력하여 위 그래프와 비교하면 더 좋다.
픽셀을 평균 낸 이미지를 모든 사진을 합쳐 놓은 대표 이미지로 생각할 수 있다.

apple_mean = np.mean(apple, axis=0).reshape(100, 100)
pineapple_mean = np.mean(pineapple, axis=0).reshape(100, 100)
banana_mean = np.mean(banana, axis=0).reshape(100, 100)

fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].imshow(apple_mean, cmap='gray_r')
axs[1].imshow(pineapple_mean, cmap='gray_r')
axs[2].imshow(banana_mean, cmap='gray_r')
plt.show()

세 과일은 픽셀 위치에 따라 값의 크기가 차이난다.
이 대표 이미지와 가까운 사진을 골라낸다면 사과, 파인애플, 바나나를 구분할 수 있을 것이다.

이처럼 흑백 사진에 있는 픽셀값을 사용해 과일 사진을 모으는 작업을 해 보았다. 이렇게 비슷한 샘플끼리 그룹으로 모으는 작업을 군집(clustering)이라고 한다. 군집은 대표적인 비지도 학습 작업 중 하나이고, 군집 알고리즘에서 만든 그룹을 클러스터(cluster)라고 부른다.

k-means

앞에서는 사과, 파인애플, 바나나에 있는 각 픽셀의 평균값을 구해서 가장 가까운 사진을 골랐다. 이 경우에는 사과, 파인애플, 바나나 사진임을 미리 알고 있었기 때문에 각 과일의 평균을 구할 수 있었다. 하지만 진짜 비지도 학습에서는 사진에 어떤 과일이 들어 있는지 알지 못한다.
이런 경우 어떻게 평균값을 구할 수 있을까? 바로 k-평균(k-means) 군집 알고리즘이 평균값을 자동으로 찾아준다.

k-means 알고리즘 작동방식

1. 무작위로 k개의 클러스터 중심을 정한다.
2. 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다.
3. 클러스터에서 속한 샘플의 평균값으로 클러스터 중심을 변경한다.
4. 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복한다.

k-means 모델 만들기

1. 데이터 준비하기

!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)

준비된 넘파이 배열을 100*10000 크기로 재배열한다.

2. k-means 알고리즘으로 모델 학습하기

사이킷런의 k-평균 알고리즘은 sklearn.cluster 모듈에 KMeans 클래스가 구현되어 있다.
n-cluster 매개변수로 클러스터 갯수를 지정할 수 있다.
3개로 지정 후 모델을 훈련시킨다.

from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruites_2d)

군집된 결과는 KMeans 객체의 labels_ 속성된 결과에 저장된다.
클러스터 갯수가 3이기 때문에 배열의 값은 0,1,2 중 하나이다.
단, 레이블값과 순서에 의미는 없다.

>>> print(km.labels_)
[2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 0 2 0 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 2 0 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1]

이를 통해 각 클러스터의 샘플의 갯수를 알 수 있다.

>>> print(np.unique(km.labels_, return_counts=True))
(array([0, 1, 2], dtype=int32), array([111,  98,  91]))

3. 각 클러스터의 그림 출력하기

각 클러스터가 어떤 이미지를 나타냈는지 그림으로 출력하기 위해 간단한 유틸리티 함수를 만들어본다.

import matplotlib.pyplot as plt

def draw_fruits(arr, ratio=1):
    n = len(arr)    # n은 샘플 개수입니다
    # 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
    rows = int(np.ceil(n/10))
    # 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
    cols = n if rows < 2 else 10
    fig, axs = plt.subplots(rows, cols,
                            figsize=(cols*ratio, rows*ratio), squeeze=False)
    for i in range(rows):
        for j in range(cols):
            if i*10 + j < n:    # n 개까지만 그립니다.
                axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
            axs[i, j].axis('off')
    plt.show()

• draw_fruits()는 (샘플갯수, 너비, 높이)의 3차원 배열을 받아 가로로 10개의 이미지를 출력하는 함수이다.
• figsize는 ratio 매개변수에 비례하여 커진다.
• draw_fruits()에 fruits 배열을 불리언 인덱싱을 통해 넣어준다.

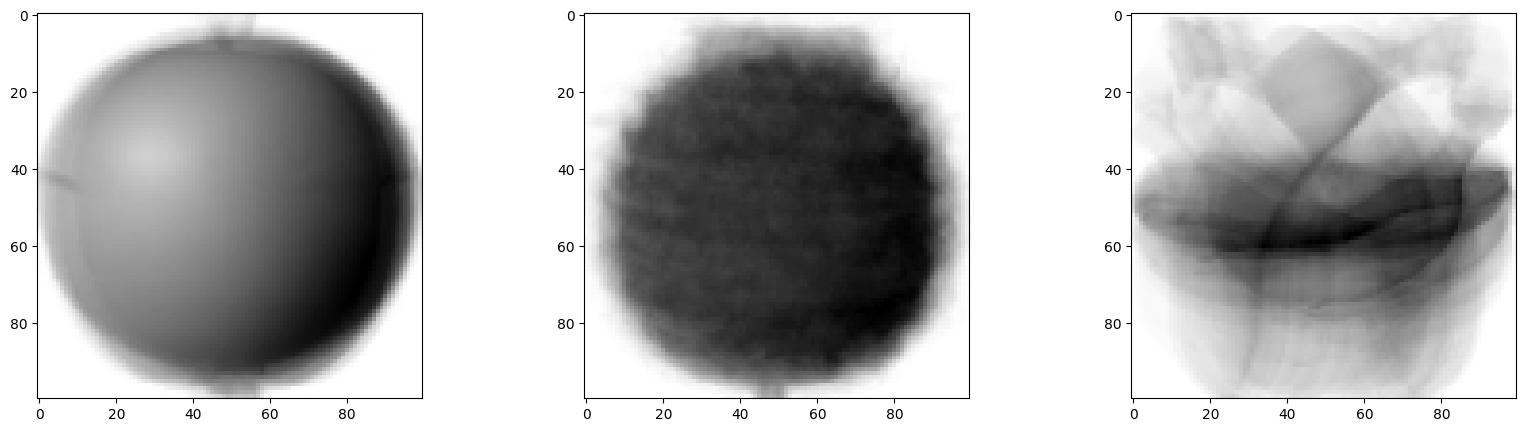
draw_fruits(fruits[km.labels_==0])

• 레이블 0에는 파인애플과 바나나, 사과가 섞여있는 것을 볼 수 있다.
• k-means 알고리즘이 이 샘플들을 완벽하게 분류하진 못했지만, 비슷한 샘플을 잘 모은 것을 볼 수 있다.

• 사과를 완벽하게 분류 했다.

4. 클러스터 중심

KMeans 클래스가 최종적으로 찾은 클러스터 중심은 cluser_centers_ 속성에 저장되어 있다.
이를 그림으로 표현해보면 아래와 같다.

draw_fruits(km.cluster_centers_.reshape(-1, 100, 100), ratio=3)

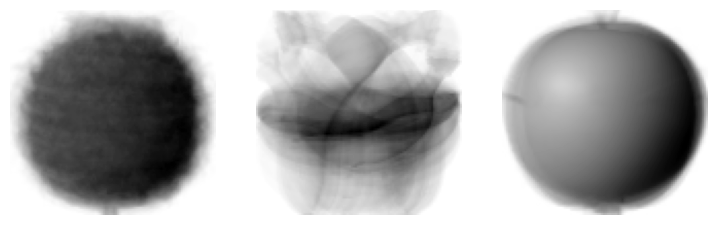
이전에 각 과일의 평균 픽셀값을 출력했던 것과 비슷함을 확인할 수 있다.

훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환해주는 transfor() 메서드와, 데이터를 예측하는 predict() 메서드가 있다.
클러스터 중심이 가장 가까운 것이 예측 클래스로 출력된다.

>>> print(km.transform(fruits_2d[100:101]))
[[3393.8136117  8837.37750892 5267.70439881]]

>>> print(km.predict(fruits_2d[100:101]))
[0]

k-means 알고리즘은 클러스터 중심을 옮기면서 최적의 클러스터를 찾는 과정을 반복하는데, 알고리즘이 반복한 횟수는 n_iter_에 저장된다.

>>> print(km.n_iter_)
4

최적의 k 찾기 : 엘보우 방법

k-means 알고리즘의 단점 중 하나는, 클러스터 갯수를 사전에 지정해야 한다는 것이다.
군집 알고리즘에서 적절한 k값을 찾는 완벽한 방법은 없다. 저마다 장단점이 있지만 가장 대표적인 엘보우 방법을 알아보겠다.

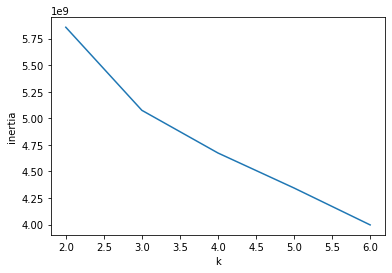
k-means 알고리즘은 클러스터 중심과 클러스터에 속한 샘플 사이의 거리를 잴 수 있는데, 이것의 제곱합을 이너셔(inertia)라고 한다.

이너셔는 클러스터에 속한 샘플이 얼마나 가깝게 모여있는지를 나타내는 값인데, 클러스터 개수가 늘어나면 이너셔도 줄어든다.

엘보우 방법은 클러스터 갯수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터를 찾는 방법이다.

클러스터 갯수에 대한 이너셔를 그래프로 그리면 꺽이는 지점이 있는데, 그 지점이 바로 적절한 클러스터 갯수이다.
KMeans 클래스는 자동으로 이너셔를 계산해서 inertia_ 속성으로 제공한다.

inertia = []
for k in range(2, 7):
   km = KMeans(n_clusters=k, random_state=42)
   km.fit(fruits_2d)
   inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()

주성분 분석

차원 축소

주성분 분석

설명된 분산